麦克洛克-皮茨神经元模型(MCP)
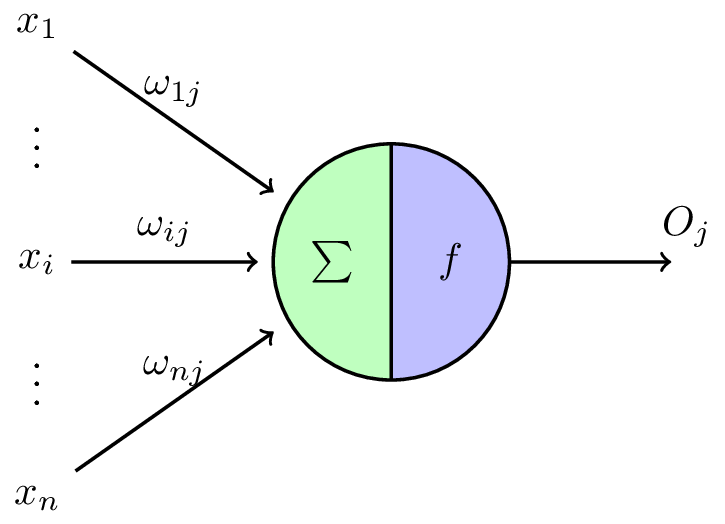
按照生物神经元,我们建立 M-P 模型。为了使得建模更加简单,以便于进行形式化表达,我们忽略时间整合作用、不应期等复杂因素,并把神经元的突触时延和强度当成常数。

结合M-P模型示意图来看,对于某一个神经元 $j$(注意别混淆成变量了,在这里 $j$ 只是起到标识某个神经元的作用),它可能接受同时接受了许多个输入信号,用 $x_i$ 表示,前面说过,由于生物神经元具有不同的突触性质和突触强度(水管粗细不同),所以对神经元的影响不同,我们用权值 $w_{ij}$ 来表示,其正负模拟了生物神经元中突出的兴奋和抑制(进水和出水),其大小则代表了突出的不同连接强度。由于累加性,我们对全部输入信号进行累加整合,相当于生物神经元中的膜电位(水的变化总量),其值就为:
$$ net_j(t+1) = \sum{w_{ij}x_i(t)} \tag1 $$
神经元激活与否(外接专用水管流出与否)取决于某一阈值电平(水位高度),即只有当其输入总和超过阈值 $T_j$ 时,神经元才被激活而发放脉冲,否则神经元不会发生输出信号。整个过程可以用下面这个函数来表示:
$$ o_j(t+1) = f{[\sum{w_{ij}x_i(t)}]-T_j} \tag2 $$
由此我们可以得到总结出M-P模型的6个特点:
- 每个神经元都是一个多输入单输出的信息处理单元;
- 神经元输入分兴奋性输入和抑制性输入两种类型;
- 神经元具有空间整合特性和阈值特性;
- 神经元输入与输出间有固定的时滞,主要取决于突触延搁;
- 忽略时间整合作用和不应期;
- 神经元本身是非时变的,即其突触时延和突触强度均为常数。
前面4点和生物神经元保持一致。为了简单起见,对膜电位的计算 $net’_j(t)$ 并没有考虑时间整合,只考虑了空间整合,即只对每条神经末梢传来的信号根据权重进行累加整合,而没有考虑输入输出间的突触时延,体现了第 5 个特点。
简化公式: $$ \begin{align} net’_j &=& W^TX \tag1 \\o_j &=& f(net) \\&=& f(W^TX) \tag2 \end{align} $$